用MATLAB研究多项式插值的振荡现象我要分享

问题提出

考虑一个固定的区间上用插值逼近一个函数。显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。我们自然关心插值多项式的次数增加时，L_n(x)是否也更加靠近被逼近的函数。龙格（Runge）给出一个例子是极著名并富有启发性的。设区间[-1,1]上函数.

实验内容及要求

考虑区间[-1,1]的一个等距划分，分点为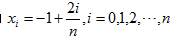，则拉格朗日插值多项式为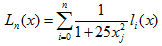.其中的l_i(x),i=0,1,2,...,n是n次拉格朗日插值基函数。

1. 首先构造不同分点数目(n=2,3….)的插值多项式函数，然后将原函数f(x)及其差值多项式函数L_n(x)的图形画在一张图上，区间为[-1，1]，比较并分析实验结果。

2.选择其他的函数，如定义在区间[-5，5]上的函数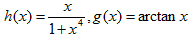，重复上述实验看其结果。

3.区间[a,b]上切比雪夫点的定义为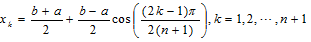，以x₁,x₂,...,x_n+1为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析原因。

实验步骤及结果分析

1. 首先构造不同分点数目(n=2,3….)的插值多项式函数，然后将原函数f(x)及其差值多项式函数的图形画在一张图上，区间为[-1，1]，比较并分析实验结果。

步骤：编制程序（test2_1_1.m）：取等距节点，计算原函数f(x)及其相应的插值函数L(x)，并将其图形画在同一张图上。取不同的插值次数n（2，4，6，8，10，12），画出各阶图形，并写出插值函数。

结果：运行文件test2_1_1.m，分别得到原函数和各次插值函数的图像，以及各次插值函数。

各次插值函数如下：

当n=2时：L=1 - (25*x^2)/26

当n=4时：L=(1250*x^4)/377 - (3225*x^2)/754 + 1

当n=6时：L=- (1265625*x^6)/96356 + (2019375*x^4)/96356 - (211600*x^2)/24089 + 1

当n=8时：L= (200000000*x^8)/3725137 - (383000000*x^6)/3725137+ (228601250*x^4)/3725137 – (98366225*x^2)/7450274 + 1

当n=10时：L= - (390625*x^10)/1768 + (109375*x^8)/221 - (51875*x^6)/136 + (54525*x^4)/442 - (3725*x^2)/221 + 1

当n=12时：L= (25628906250000*x^12)/28167484501 - (65809335937500*x^10)/28167484501+ (62017871484375*x^8)/28167484501 - (107641853578125*x^6)/112669938004+ (367051586875*x^4)/1847048164 - (551599221900*x^2)/28167484501+ 1

原函数及各次插值函数图像：

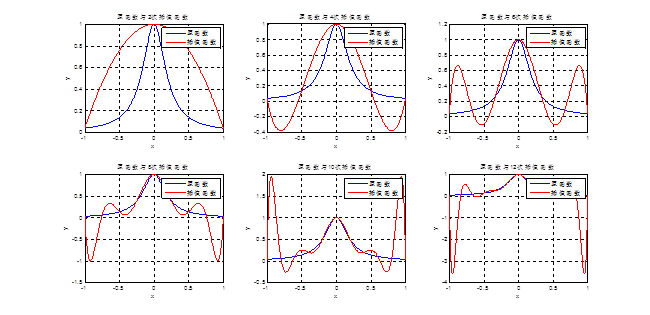
结果分析：

①从上面插值函数可知：

由于原函数为偶函数，所以插值函数也为偶函数，这一点从插值函数L(x)中有所体现，其奇次项权威领。

随着插值次数的增加，插值函数的次数和项数也在增加，其复杂性也在增加，同时计算次数也在增加，由于计算机位数限制而引入的计算误差也在增加。

②从上面的图可以看出：

当差值次数较低（n=2）时，插值函数和原函数还不能吻合，随着次数的增加插值函数越来越逼近与原函数，次数越高插值函数越吻合原函数，但是这只局限于插值区间的中间部分。

在靠近插值区间的两端边界时，随着次数n的增大，插值函数在边界附近出现极大的波动。如，n=4时其波动幅度小于0.4，而当n=12时其波动幅度大约超过3了。这就使得插值函数在边界的误差随着次数n的增大越来月显著的越加，从而插值函数越来越不准确，与原函数越来越不吻合。

从以上分析可以得出：在拉格朗日基函数的高次插值中，在插值区间的边界部分插值函数会出现很大波动，明显偏离原函数，所以拉格朗日插值次数不宜过高。

此外，我们把高次插值边界出现这种波动的现象叫做龙格现象，龙格现象说明插值不准确，在实际中要尽量避免。通常为避免出现龙格现象可以采用分段低次插值或采用切比雪夫零点插值。

2. 分别选择h(x)=x/(1+x⁴), g(x)=arctan(x)两个函数，定义在区间[-5，5]上，重复上述实验。

步骤：编制程序只需在上一问的基础上稍作修改即可。同样取等距节点，其中文件test2_1_2_1.m为与函数h(x)对应程序，次数n（2,4,6,8,10,12）。其中文件test2_1_2_2.m为与函数g(x)对应程序，次数n（2,6,10,18,22）。

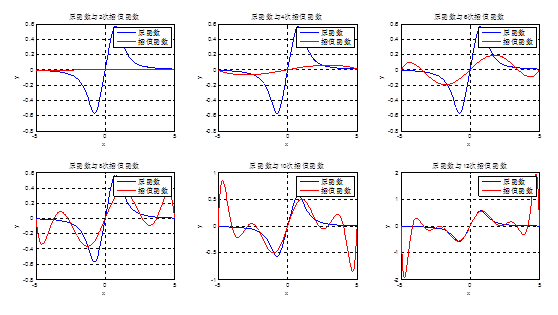
结果：①原函数h(x)=x/(1+x⁴)及各次插值函数图像（程序test2_1_2_1.m）

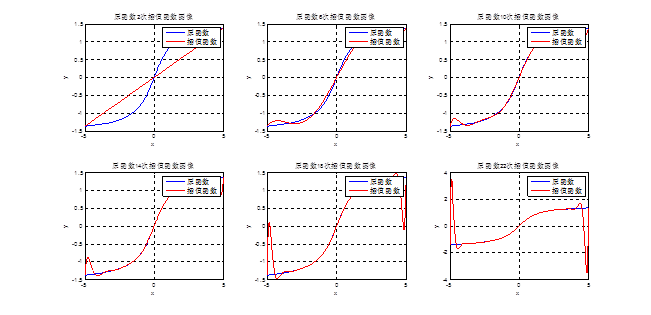
②原函数g(x)=arctan(x)及各次插值函数图像：（程序test2_1_2_2.m）

结果分析：

①由于以上的两道原函数都为奇函数，所以其插值函数也比为奇函数，即插值函数偶次幂项为零。（由于篇幅问题，具体插值函数不在报告中给出，可以由程序输出LL得出）此外，其插值函数的多项式也会随着插值次数的增加而增加，由此而带来的误差也会随之而增大。

②有上面两幅图可以得出：和上一问出现差不多同样的问题，在较低次插值时，插值函数与原函数之间的误差较小，它们之间也比较吻合，如n=10时，插值函数与g(x)=arctan(x)原函数逼近的很好，虽然边界出已出现误差增大，但相对还是较小可以接受，但是高次插值时，插值区间边界区域的误差急剧增大，龙格现象再次出现，而且随着n的增大越来越严重。

③综上，在等距节点的拉格朗日插值中，插值次数不易过高，在高次插值中龙格现象无法避免，而且超过一定次数后，龙格现象会越来越严重。为解决龙格现象可以采用分段低次插值或采用切比雪夫零点最为插值点。

3.区间[a,b]上切比雪夫点的定义为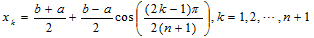,本次采用切比雪夫零点x₁,x₂…x_n+1为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析原因。

步骤：

编制程序，只需做局部修改，将等距节点替换为切比雪夫零点作为插值节点。其他基本不变。其中其中文件test2_1_3_1.m为与函数f(x)对应程序，次数n（2,4,6,8,10,12）。其中文件test2_1_3_2.m为与函数h(x)对应程序，次数n（2,4,6,8,10,12）。其中其中文件test2_1_3_3.m为与函数g(x)对应程序，次数n（2,6,10,18,22）。

结果：

①原函数，区间[-1,1]，次数n（2,4,6,8,10,12），（程序test2_1_3_1.m）。原函数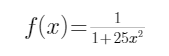

②原函数h(x)=x/(1+x⁴)，区间[-5,5]，次数n（2,4,6,8,10,12），（程序test2_1_3_2.m）。原函数及各次插值函数的图像：

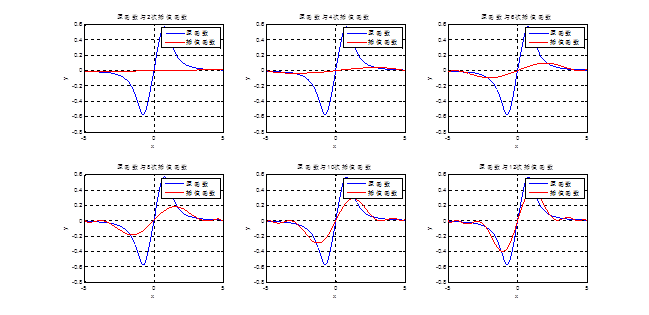
③原函数g(x)=arctan(x)，区间[-5,5]，次数n（2,6,10,18,22），（程序test2_1_3_3.m）。原函数及各次插值函数的图像：

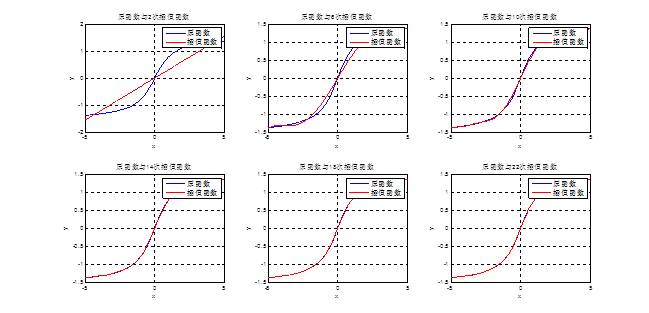
分析：

从上面的三个图可以得出：

①当原函数与插值函数的奇偶性相同，原函数为奇函数则插值函数也为奇函数，原函数为偶函数则插值函数也为偶函数。

②可以看出当插值次数较小时原函数与插值函数不太吻合，随着n的增大插值函数越来越逼近原函数。在插值次数较低时误差主要出现在中间部分，随着n的增大中间部分误差较小，插值函数逼近原函数的程度越好。而且整个过程中插值区间的边界部分误差一直较小。

③在插值区间的边界没有出现龙格现象。本次插值与前面插值的主要区别是插值节点的选择不同，其他条件都一样。由此可以看出龙格现象的出现还与节点的选取有关。

但是为什么切比雪夫零点作为插值节点时就可以避免龙哥现象呢？这我们还得从切比雪夫零点的定义看起。切比雪夫插值点定义为

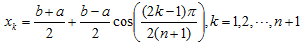
可以看出切比雪夫点恰好是以为圆心，以为半径的圆的上半部分圆周上等距分布的点，而对应到横坐标就是切比雪夫零点，其表现是在接近区间的两端很密集。前面等距节点的高次插值中，在插值区间两端出现龙格现象，两端误差较大，这就需要在两端用更多的点来插值才可以减小误差，而切比雪夫零点解决了这个问题，所以用切比雪夫零点插值可以很好的避免出现龙格现象，切比雪夫零点要比等距节点更好。

附录：程序代码

注意：一下各个m文件保存在相同目录下。

附录一：test2_1_1.m文件源码

for n=2:2:12               %n为插值阶数
subplot(2,3,n/2)           %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
f=1/(1+25*x^2);            %原函数  
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=-1+2*i/n;      %划分等距节点
end
for j=0:n
    for i=0:n
     if i~=j               %求插值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1));   
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(1/(1+25*x1(j+1)^2));     %插值函数
end
LL(n)=simplify(L);        %插值函数化简
x=-1:0.01:1;
y1=subs(f,x);             %将x带入原函数f中
y2=subs(L,x);             %将x带入插值函数L中
plot(x,y1,'b'); hold on;
plot(x,y2,'r'); hold off;
title(['原函数与',num2str(n),'次插值函数']);
xlabel('x'); ylabel('y');
legend('原函数','插值函数');
grid on
end

附录二：test2_1_2_1.m文件源码

for n=2:2:12              %n为插值阶数
subplot(2,3,n/2)           %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
h=x/(1+x^4);               %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=-5+10*i/n ;    %划分等距节点
end
for j=0:n
    for i=0:n
     if i~=j               %求插值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1)); 
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(x1(j+1)/(1+x1(j+1)^4));     %插值函数
end
LL(n)=simplify(L);         %插值函数化简
x=-5:0.01:5;
y1=subs(h,x);              %将x带入原函数f中
y2=subs(L,x);              %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数与',num2str(n),'次插值函数']);
xlabel('x'); ylabel('y');
legend('原函数','插值函数');
grid on
end

附录三：test2_1_2_2.m文件源码

for n=2:4:22               %n为插值阶数
subplot(2,3,(n+2)/4)       %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
h=atan(x);                 %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=-5+10*i/n ;    %划分等距节点
end
for j=0:n
    for i=0:n
     if i~=j               %差值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1));      
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(atan(x1(j+1)));   %插值函数
end
%  LL(n)=simplify(L);太费时了  
x=-5:0.01:5;
y1=subs(h,x);              %将x带入原函数h中
y2=subs(L,x);              %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数',num2str(n),'次插值函数']);
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
end

附录四：test2_1_3_1.m文件源码

for n=2:2:12               %n为插值阶数
subplot(2,3,n/2)           %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
f=1/(1+25*x^2);            %原函数 
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=cos((2*i+1)*pi/(2*(n+1)));    %切比雪夫零点
end
for j=0:n
    for i=0:n
     if i~=j               %求插值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1));
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(1/(1+25*x1(j+1)^2));      %插值函数
end
LL(n)=simplify(L);        %插值函数化简
x=-1:0.01:1;
y1=subs(f,x);             %将x带入原函数f中
y2=subs(L,x);             %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数与',num2str(n),'次插值函数图像']);
xlabel('x');ylabel('y');
legend('原函数','插值函数');
grid on
end

附录五：test2_1_3_2.m文件源码

for n=2:2:12              %n为插值阶数
subplot(2,3,n/2)          %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
h=x/(1+x^4);              %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=5*cos((2*i+1)*pi/(2*(n+1)));     %切比雪夫零点
end
for j=0:n
    for i=0:n
     if i~=j             %求插值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1));
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(x1(j+1)/(1+x1(j+1)^4));     %插值函数
end
LL(n)=simplify(L);         %插值函数化简
x=-5:0.01:5;
y1=subs(h,x);              %将x带入原函数f中
y2=subs(L,x);              %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数与',num2str(n),'次插值函数']);
xlabel('x'); ylabel('y');
legend('原函数','插值函数');
grid on
end

附录六：test2_1_3_3.m文件源码

for n=2:4:22               %n为插值阶数
subplot(2,3,(n+2)/4)       %将各阶原函数与插值函数的图像分别一张图片上面。
syms x;
h=atan(x);                 %原函数
x1=sym(zeros(n+1));
W=sym(ones(n+1));
L=sym(0);
for i=0:n
    x1(i+1)=5*cos((2*i+1)*pi/(2*(n+1)));     %切比雪夫零点
end
for j=0:n
    for i=0:n
     if i~=j              %差值基函数
         w=(x-x1(i+1))/(x1(j+1)-x1(i+1));
         W(j+1)=W(j+1)*w;
     end
    end
      L=L+W(j+1)*(atan(x1(j+1)));             %插值函数
end
%  LL(n)=simplify(L);太费时了  
x=-5:0.01:5;
y1=subs(h,x);              %将x带入原函数h中
y2=subs(L,x);              %将x带入插值函数L中
plot(x,y1,'b');hold on;
plot(x,y2,'r');hold off;
title(['原函数与',num2str(n),'次插值函数']);
xlabel('x'); ylabel('y');
legend('原函数','插值函数');
grid on
end