正多边形是一种非常漂亮的几何图形,在很多场合我们都可以看到各种多边形。所谓正多边形就是所有角都相等、并且所有边都相等的简单多边形,简单多边形是指在任何位置都不与自身相交的多边形。下面就像大家介绍一种用matlab画奇数多边形的方法。
1.正多边形的性质,下表总结了正多边形的各项性质,如下表所示:
内角 |
正n边形的内角和度数为:(n-2)×180度; 正n边形的一个内角是(n-2)×180°÷n. |
外角 |
正n边形外角和等于n·180°-(n-2)·180°=360° 所以正n边形的一个外角为:360÷n. 所以正n边形的一个内角也可以用这个公式:180°-360÷n. |
中心角 |
任何一个正多边形,都可作一个外接圆,多边形的中心就是所作外接圆的圆心,所以每条边的中心角,实际上就是这条边所对的弧的圆心角,因此这个角就是360度÷边数。 正多边形中心角:360÷n |
对角线 |
在一个正多边形中,一个点可以与除了与他相邻的所有点连线,就成了点数减2(2是那两个相邻的点)个三角形。而正多边形的点数与边数相同,所以有边数减2个三角形。三角形内角和:180度,所以把边数减2乘上180度,就是这个正多边形的内角和对角线 对角线数量的计算公式:n(n-3)÷2。 |
面积 |
设正n边形的半径为R,边长为an,中心角为αn,边心距为r n。则αn=360°÷n,an=2Rsin(180°÷n),r n=Rcos(180°÷n),R^2=r n^2+(an÷2)^2,周长pn=n×an,面积Sn=pn×rn÷2。 |
对称轴 |
奇数边:连接一个顶点和顶点所对的边的中点,即为对称轴; 偶数边:连接相对的两个边的中点,或者连接相对称的两个顶点,都是对称轴。 正N边形边数为N。正N边形角数为N。正N边形对称轴数,奇数为N;偶数为2N。 |
2.画出奇数正多边形,下图所示的是用matlab画奇数正多边形的代码,分别演示了正常排序和非正常排序所画出的结果。如下图所示:
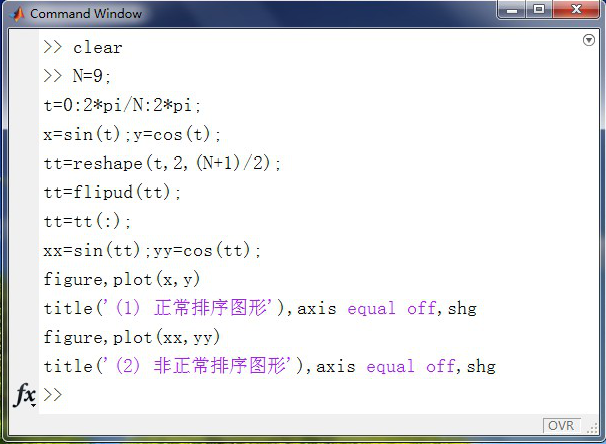
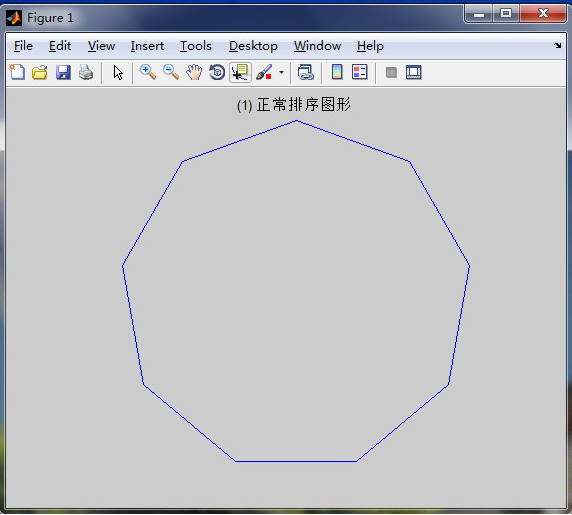
3.正常排序的图形:
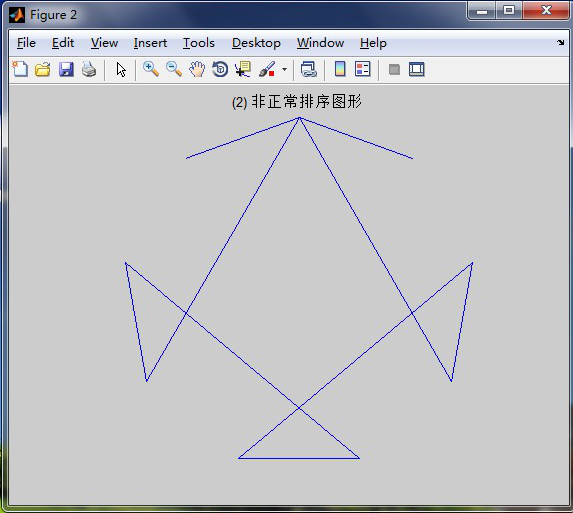
4:非正常排序的图形: